Архив рубрики: ‘Методики создания экологических карт’
ВИКОРИСТАННЯ МЕТОДУ ІНТЕРПОЛЯЦІЇ МОДУЛЯ VERTICAL MAPPER (MAPINFO) ПРИ ВИРІШЕННІ КАРТОГРАФІЧНИХ ЗАДАЧ ҐРУНТОЗНАВСТВА
При побудові ґрунтових картосхем, цифрових моделей рельєфу доволі часто виникає потреба у побудові тривимірної моделі рельєфу що дозволяє поліпшити візуалізацію цифрових моделей та проводити їх аналіз, вирішувати питання локалізації нерівностей на полі, тобто уточнювати мікрорельєф поля (наприклад степових блюдець). Модуль Vertical Mapper призначений для побудови дво- та тривимірних моделей природних явищ, процесів та їх подальшу візуалізацію та аналіз.
Процес інтерполяції дозволяє розрахувати значення в «поверхні», який використовує математичний апарат, користуючись даними, які взяті з бази даних. Нові значення розраховуються на основі існуючих даних, які просторо розташовані на «поверхні» по принципу «заповнення дірок, що пустують» між існуючими точками. При такому виді розрахунку може бути використано інтерполяції значень в «поверхні». Таке рішення має не досить достовірну основу тому що залежить від даних на основі яких він буде проводитися. Тому застосувавши новий варіант інтерполяції можна буде спостерігати кожен раз нову «поверхню» на базі тих самих даних. Тому щоб полегшити вибір варіанту інтерполяції, які будуть застосовуватися в тому чи іншому випадку нижче наведено таблицю, яка допоможе при виборі оптимального типу інтерполяції (див.табл.1)
Тип інтерполяції | Короткий опис типу інтерполяції |
| Дані які використовуються об’єднуються в сітку з ліній, які створюють сітку з багатокутників (чи трикутників), які названі Нерегулярною Тріангуляційною Сіткою (TIN). Ця сітка представлена оригінальною розрахованою поверхнею. Нові значення в цьому типі поверхні розраховуються згідно значень найближчих точок, які відомі. |
| Вихідні дані, які знаходяться в визначеному користувачем радіусі потрапляють у вузол нової поверхні у виді середнього математичного зваженого між найближчими точками, які потрапили в цей радіус. |
| Поверхня звичайної інтерполяції будується на базі (діаграм Вороного) [1] й використовує оригінальні дані. Створюється поверхня з розрахунку впливу кожного значення в точці й використовується у вузлі новоствореної поверхні. Звичайна інтерполяція (проста): Складається з двох кроків виконання процесу інтерполяції. Практично всі перемінні виконані у вигляді перед установок й полегшує роботу користувача у розподіленні точок. Удосконалена: Надає доступ до більш повної консолі керування процесом звичайної інтерполяції. (таких як: уточнене корегування поверхні, яка створена з точкового файлу). |
| Вихідні дані з’єднуються в сітку з ліній створює прямокутники. Нові значення поверхні розраховуються використовує нахил (тобто нахил подвійного набору ліній (полі ліній), які формуються з найближчих точок. |
| Метод геостатичного процесу інтерполяції, який включає два параметра: відстань й градус зміни між відомими точками. Між ними розраховується значення у вузлі поверхні в невідомому просторі. Графічні інструменти даної інтерполяції допомагають зрозуміти напрям зміни даних моделі (тобто північ-південь, схід-захід). |
| Значення вузлів поверхні розраховуються на основі встановлених користувачем математичних операторів, використавши дані точок, які знайдені в заданому радіусі навколо кожної точки. Математичні оператори включають: підсумовування, мінімальне значення, максимальне значення, середнє значення й медіану. |
Вибір типу інтерполяції. Доволі часто перед побудовою поверхні важко визначитися з вибором методу інтерполяції. Результат побудови не відображає реальної ситуації, й як наслідок, не задовольняє користувача. Тому, перед тим, як приступати до побудови поверхні необхідно вирішити наступні питання:
1. Що необхідно отримати в результаті побудови поверхні? Деякі інтерполяції можуть автоматично застосовуватися в залежності від мети побудови поверхні. Нижче в таблиці 2 наведені подібні випадки застосування поверхонь.
Результат застосування інтерполяції | Тип інтерполяції, що застосовується |
Цифрова модель рельєфу | Тріангуляція з згладжуванням (TIN) Triangulation with Smoothing, Звичайна інтерполяція (Natural Neighbour) |
Хімія ґрунтів (або агрохімія) | Зворотне дистанційне середнє (IDW) Inverse Distance Weighting, Інтерполяція Криггинга (Kriging) |
Міграція хімічних елементів | Звичайна інтерполяція (Natural Neighbour), Зворотне дистанційне середнє (IDW) Inverse Distance Weighting, Інтерполяція Криггинга (Kriging) |
Розподіл важких елементів | Звичайна інтерполяція (Natural Neighbour) |
2. Яка повинна бути точність даних? Різні інтерполяції по різному працюють з вихідними даними. Деякі припускають, що точкові дані з бази даних вже достовірні, а інші ні. Від точності вихідних даних також залежить вибір інтерполяції (див.табл. 3).
Точність вихідних даних | Можливий варіант інтерполяції |
Точні | Тріангуляція з згладжуванням (TIN) Triangulation with Smoothing, Звичайна інтерполяція (Natural Neighbour), Прямокутна Rectangular (Bilinear) | Не точні чи не достатньо точні | Зворотне дистанційне середнє (IDW) Inverse Distance Weighting, Інтерполяція Криггинга (Kriging) |
3. Який візуальний розподіл точок на вихідній поверхні? Деякі інтерполяції «виробляють» більш точні поверхні, коли розподіл точок має випадковий чи хаотичний характер, інші коли точки розподілені регулярно.
Вид точкового розподілення | Можливий процес інтерполяції |
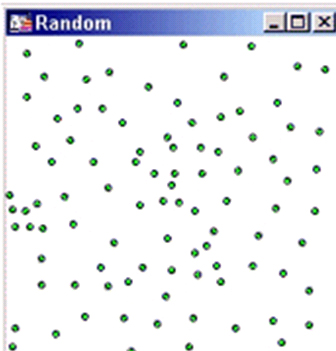
Більшість інтерполяцій працює з випадково розподіленими точковими даними. | |
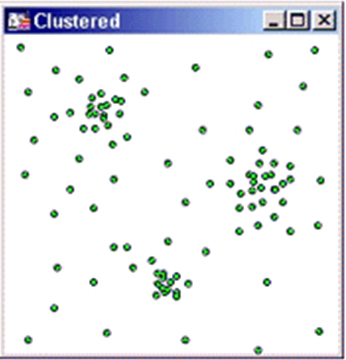
Високо згруповані дані, як правило, створюють проблеми для користувача. Можливі інтерполяції для застосування: Звичайна інтерполяція (Natural Neighbour), Зворотне дистанційне середнє (IDW) Inverse Distance Weighting, Інтерполяція Криггинга (Kriging), Тріангуляція з згладжуванням (TIN) Triangulation with Smoothing. | |
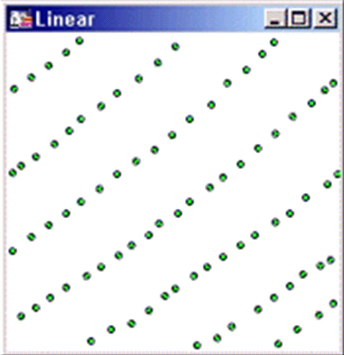
Гратчастий вид даних може бути отримано тільки з просторово точного зразка. Можливі інтерполяції для застосування: Прямокутна Rectangular (Bilinear), Звичайна інтерполяція (Natural Neighbour), Інтерполяція Криггинга (Kriging). | |
Цей тип лінійної поверхні отримується шляхом аерофотозйомки. Можливі інтерполяції для застосування: Зворотне дистанційне середнє (IDW) Inverse Distance Weighting, Звичайна інтерполяція (Natural Neighbour), Інтерполяція Криггинга (Kriging). | |
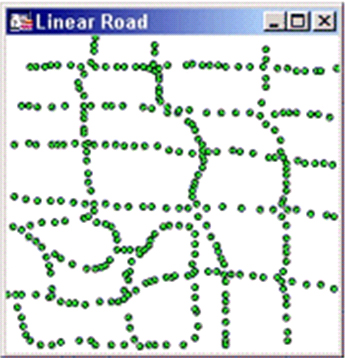
Цей тип просторового розподілу отримується, коли зразки даних розподіляються вздовж доріг. Можливі інтерполяції для застосування: Звичайна інтерполяція (Natural Neighbour), Інтерполяція Криггинга (Kriging). |
4. Які фактори можуть обмежувати швидкість інтерполяційного процесу? Більш менший вузол в поверхні й/чи більша кількість точок все це забирає більше часу на розрахунки. Причому деякі інтерполяції швидші за інших.
Тип інтерполяції | Швидкість | Обмежуючий фактори |
Тріангуляція з згладжуванням (TIN) Triangulation with Smoothing | Швидкісна | Пошук й візуалізація розміру радіуса |
Зворотне дистанційне середнє (IDW) Inverse Distance Weighting | Швидкісна | Пошук й візуалізація розміру радіуса |
Прямокутна Rectangular (Bilinear) | Дуже швидкісна | Пошук розміру радіуса |
Звичайна інтерполяція (Natural Neighbour) | Повільна | Розподіл точок |
Інтерполяція Криггинга (Kriging) | Повільна | Числа и напрям аналізу |
1.Наведені положення в статті дозволяють використовуючи таблиці вибрати необхідний для аналізу тип інтерполяції.
2. Спираючись на дані таблиць вибір типу інтерполяції має високий ступінь репрезентативності.
Література:
1. Діаграми Вороного. Режим доступу до журналу: http://ru.wikipedia.org/wiki/Диаграмма_Вороного
2. Технічна документація модулю Vertical Mapper. Режим доступу до журналу: [email protected]
3. Лурье И.И. Основы геоинформатики и создание ГИС //Дистанционное зондирование и географические информационные системы / Под. ред. А.М. Берлянта. – Ч.1. – М.: ООО «ИНЭКС)92», 2002. – 140 с.
4. Митчелл Э. Руководство по ГИС)анализу. – Ч.1: Пространственные модели и взаимосвязи.Ї К: ЗАО ЕСОММ Со; Стилос, 2000. – 198 с.
 Тріангуляція з згладжуванням (TIN) Triangulation with Smoothing
Тріангуляція з згладжуванням (TIN) Triangulation with Smoothing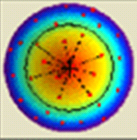 Зворотне дистанційне середнє (IDW) Inverse Distance Weighting
Зворотне дистанційне середнє (IDW) Inverse Distance Weighting Звичайна інтерполяція (проста й удосконалена) Natural Neighbour (simple and advanced)
Звичайна інтерполяція (проста й удосконалена) Natural Neighbour (simple and advanced) Прямокутна Rectangular (Bilinear)
Прямокутна Rectangular (Bilinear)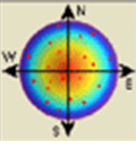 Інтерполяція Криггинга (Kriging)
Інтерполяція Криггинга (Kriging) Точкова користувача (Custom Point Estimation)
Точкова користувача (Custom Point Estimation)